Fibonaççi ardicilliqlari – Orta əsrlərin ən böyük İtalyan riyaziyatçılarından olan Leanardo Fibonaççinin yaşadığı dövrdə üç kitab yazmışdır və onlardan ən önəmlisi “Liber Abacci”dir. Kitab, günümüzdə “Fibonaççi ədədləri” olaraq tanınan “1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144….” şəklində sonsuza qədər gedən rəqəmlər ardıcıllığının, problemlərin həllində istifadə edilməsi izah olunur.
Ralph Elliot isə “Təbiət Qanunlar” kitabında təbiətdəki qanunauyğunluqlardan ilham aldığını, hətta onların insan fəaliyyətlərinə belə təsir etdiyini iddia edirdi. O, yeni nəzəriyyənin riyazi bazası olaraq XIII əsrdə yaşamış Fibonaççinin rəqəmsal düzülməsini araşdımış və bu ardıcıllığı “Fibonaççi ədədləri” adlandırmışdır.
Silsilədə yerləşən hər Fibonaççi sayı özündən əvvəlki ədədlərlə riyazi olaraq əlaqəlidir.
Qizil nisbət
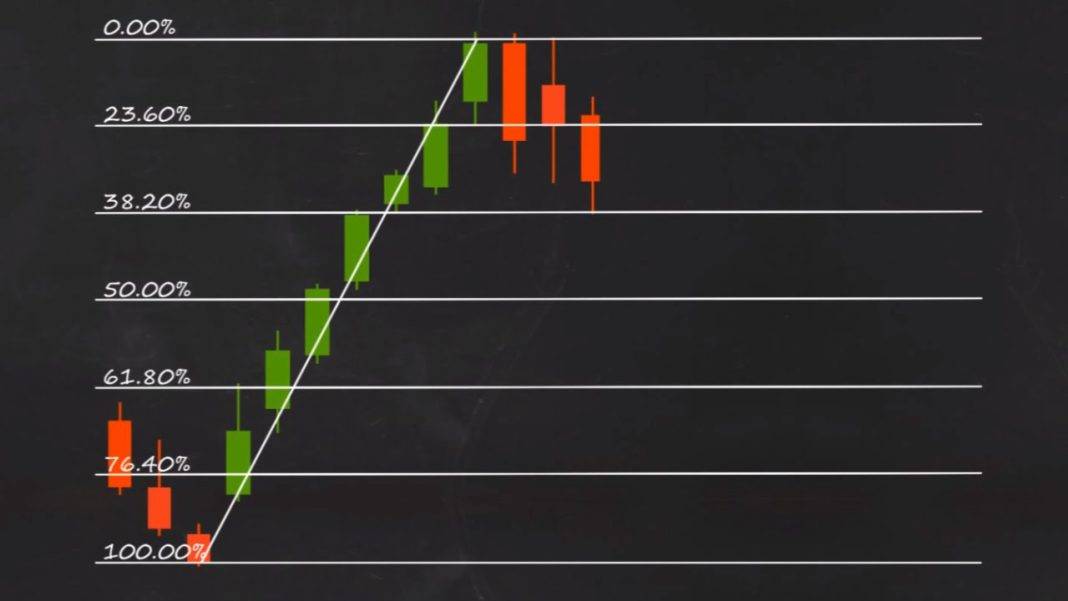
Ardıcıllıqdakı ilk bir neçə rəqəmdən sonra gələn hər bir rəqəmin özündən sonrakı rəqəmə nisbəti təqribən 0.618 ədədinə bərabərdir. Hər rəqəmin özündən əvvəlki rəqəmə nisbəti təqribən 1.618 ədədinə bərabərdir. Bu şəkildə Fibonnaççi ədədləri arasında əldə edilən 1.618 və ya 0.618 nisbətinə “Qızıl Nisbət” adlanır.
Təbiətə baxdığımızda hər yerdə Qızıl nisbət görə bilərik. Məsələn, İnsan bədəninin göbək ilə ayağı arasındakı məsafə belə insan boyunun 1,618-nə bərabər gəlir.
Fibonaççi ardicilliqlarinin xüsusiyyətləri
1) Silsilədə yer alan hər sayı özündən əvvəl gələn iki ədədin cəminə bərabərdir.
Məsələn: 3+5=8 5+8=13 və s.
2) Fibonaççi say Dördüncü rəqəmdən sonra gələn hər bir rəqəmin özündən sonrakı rəqəmə nisbəti 0.618 ədədinə yaxınlaşır.
Məsələn: 3/5=0,6 5/8=0,625 8/13=0,615 13/21=0,619 vb.
3) Düzülüşün içindəki hər ədədi özündən əvvəl gələn ədədə bölərək irəliləsəniz çıxılacaq nəticə 1,615 rəqəminə davamlı yaxın olacaq.
Məsələn: 13:8=1,625 21:13=1,615 34:21= 1,619
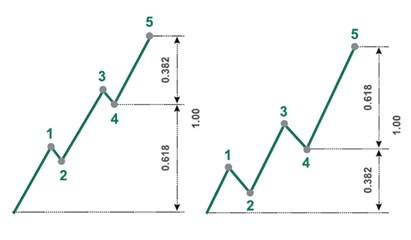
4) Rəqəm böyüdükcə müvafiq nisbət 0.618 və ya 1.618 ədədinə yaxınlaşır. Sıradakı hər bir rəqəmin özündən bir rəqəm sonrakı mövqedə yerləşmiş rəqəmə nisbəti 0.382 ədədinə, özündən bir rəqəm əvvəlki mövqedə yerləşmiş rəqəmə nisbəti isə 2.618 ədədinə yaxınlaşır.
Məsələn: 13:34=0,382 34:13=2,615
5) Fibonaççi ədədləri maliyyə bazarlarında da qiymət səviyyəsini müəyyən etməyə kömək edir. İlk qiymət hərəkəti sonra gələn, düzəltmə sonrasından ibarət olan yeni hərəkət özündən əvvəlki hərəkət dalğasının 1.618 qatına qədər davam edə bilər.
Qizil nisbət və Elliot dalğa nəzəriyyəsi
Elliot dalğa nəzəriyyəsinin riyazi təməlini Fibonaççi ədədləri meydana gətirməkdədir. Ən sadə fiqurlarda belə təməl dalğa formasının Fibonaççi ədədlərinə bölündüyünü müşahidə edə bilərik.
Məsələn:
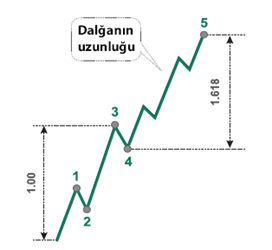
1 əsas trend 5 dalğalı bir formaya sahibdir. Dövrü tamamlayan dalğalar 2 yerə bölünür: Hərəkətverici Dalgalar (rəqəmlərlə göstərilir) və hərəkət dalğalarının ardından gələn korreksiya dalğaları (hərflərlə göstərilir).
3 növ sadə dalğa modeli mövcuddur:
Beş dövrlü dalğa, Üçlük və Üçbucaq.
5 əsas dalğa modeli mövcudur:
Hərəkətverici dalğalar, diaqonal üçbucaqlar, Ziqzaqlar, İkqat Ziqzaqlar, üçqat Ziqzaqlar
Mütənasib analiz üsulu
Mütənasib analiz üsulu, ard arda gələn qiymət dalğalarının hərəkət və zaman intervalları arasındakı mütənasib əlaələri incələyən analiz üsuludur.
Bu analiz üsuluna dayanaraq qiymət və zaman baxımından ayrı-ayrı dalğalar arasında sıx görülən bəzi dəqiq proporsional əlaqə səviyyələri təsbit edilmişdir.
Ümumi dalğalar arasındakı proporsional əlaqə iki qrupa ayrılır: Hərəkət dalğaları ilə geri alış səviyyələri arasında proporsional əlaqə və daxili quruluş dalğaları arasındakı qarşılıqlı proporsional əlaqə.
Hərəkət dalğaları arasındaki fibonaççi nisbətləri
- 3-cü dalğadan sonra meydana gələcək 5-ci dalğa boy etibarı ilə 1-ci dalğaya bərabər və ya bu dalğanın 0,618 qatı olacaq.
Hər hansı bir siklın 3 təsiredici dalğalar arasındakı əlaqələri 1,618 və 2,618 Fibonaççi nisbətlərində olduqca təsirlidir.
- 3-cü dalğadan sonra meydana gələcək 5-ci dalğa boy etibarı ilə 1-ci dalğaya bərabər və ya bu dalğanın 0,618 qatı olacaq.
Hər hansı bir siklın 3 təsiredici dalğalar arasındakı əlaqələri 1,618 və 2,618 Fibonaççi nisbətlərində olduqca təsirlidir.
Dalğa siklının arasındaki fibonaççi nisbətləri
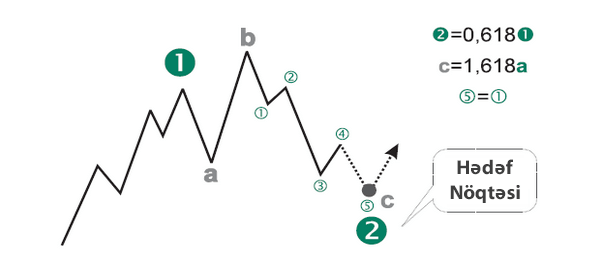
Daha əvvəl də bəhs edildiyi kimi hər hansı bir zaman intervalında müəyyən bir qiymət qrafiki bölgəsində çoxlu sayda Fibonaççi əlaqəsi aşkar oluna bilər. Hədəflədiyimiz nöqtə fərqli səviyyələrdəki dalğa əlaqələri istiqamətində birdən çox Fibonaççi nisbəti ilə doğrulana bilirsə ticarət siqnalı təsirini artırmış olur.
Məsələn: Hədəf nöqtəsi ən üst dalğa səviyyəsindəki 2-ci dalğanın 1-ci dalğanı 0.618 nisbəyi qədər geri aldığı hissəyə rast gəlirsə, bu nöqtədə korreksiya siklindəki “a” dalğasının 1.618 nisbəti qədər uzanan “c” dalğası bitirsə və yenə də bu nöqtədən “c” dalğasının daxili quruluşunu əmələ gətirən 5-ci dalğa 1-ci dalğa ilə bərabərdirsə, həmin hədəf nöqtəsində mövcud istiqamətin tamamlanacağı və bazarın yeni istiqamətə girəcəyi hesab oluna bilər.
Göründüyü kimi maliyyə birjalarında da təbiətin bir qanunauyğunluğu olan Qızıl nisbəti qorunur və bundan əmələ gələn Fibanaççi Nisbəti özünü büruzə verir. Fibonnaçi ədədləri ardıcıllığına söykənən mütənasib analiz üsulu hər zaman Elliot Dalğa Nəzəriyyəsinin əsas qaydaları ilə uyğundur.
Mənbə: İnvestaz