Vahid məbləğin bugünkü dəyəri, gələcəkdə bizə vəd edilən pulun bu günki dəyəri haqqında məlumat verən konsepsiyadır. Aşağıdakı düstürla hesablanır:

PV = FV * (1+ i) -n

PV – bugünkü dəyər

FV – gələcək dəyər

i – faiz dərəcəsi

n – dövr, müddət

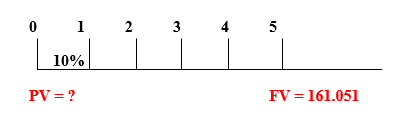
Misal: əgər 5 il sonra bizə 161.051 AZN pul lazımdırsa, bankın faiz dərəcəsinin 10% olduğunu və faizlərin illik hesablandığını nəzərə alsaq, bu gün bizə nə qədər depozit yatırmaq lazımdır:

FV = 161.051

i = 10% və ya 0.1

n = 5

PV = ?

PV = 161.051 * (1+ 0.1) -5 = 100

Bizim haqqında danışdığımız bugünki dəyər faiz illik hesablanmaq şərtilə idi. Bəs faiz rüblük və ya dəvamlı hesablandıqda bugünki dəyər nə cür tapılacaq? Gəlin bunlara tək-tək izah verək:

Vahid məbləğin bugünki dəyəri (faiz rüblük hesablandıqda)

Misal: əgər 5 il sonra bizə 161.051 AZN pul lazımdırsa, bankın faiz dərəcəsinin 10% olduğunu və faizlərin rüblük hesablandığını nəzərə alsaq, bu gün bizə nə qədər depozit yatırmaq lazımdır:

İlk olaraq, müddəti və faizi tapaq. Faizlər rüblük hesablandığı üçün müddət N=5(il)*4(rüb)=20. Bizə verilən faiz illik faiz olduğu üçün rüblük faizimiz I/Y=10%(illik faiz)/4(rüb)=2.5%.

FV = 161.051

i = 2.5% və ya 0.025

n = 20

PV = ?

PV = 161.051 * (1+ 0.025) -20 = 98.284

Vahid məbləğin bugünki dəyəri (faiz davamlı (continious) hesablandıqda)

Misal: əgər 5 il sonra bizə 161.051 AZN pul lazımdırsa, bankın faiz dərəcəsinin 10% olduğunu və faizlərin davamlı (continious) hesablandığını nəzərə alsaq, bu gün bizə nə qədər depozit yatırmaq lazımdır:

Faizlərin davamlı (continious) hesablandığı halda bugünki dəyər aşağıdakı düstürla hesablanır:

PV=FV*e -RT

PV – bugünkü dəyər

FV – gələcək dəyər

R-faiz dərəcəsi

T-müddətdir

PV=161.051*e -0.1*5 = 97.682

Alınan nəticələrdən də görünür ki, faizlərin hesablanma periodu artdıqcan pulun bugünkü dəyəri azalır.

http://innab.org/